Homoplasy corrected estimation of genetic similarity from AFLP bands, and the effect of the number of bands on the precision of estimation

Abstract

AFLP is a DNA fingerprinting technique, resulting in binary band presence–absence patterns, called profiles, with known or unknown band positions. We model AFLP as a sampling procedure of fragments, with lengths sampled from a distribution. Bands represent fragments of specific lengths. We focus on estimation of pairwise genetic similarity, defined as average fraction of common fragments, by AFLP. Usual estimators are Dice (D) or Jaccard coefficients. D overestimates genetic similarity, since identical bands in profile pairs may correspond to different fragments (homoplasy). Another complicating factor is the occurrence of different fragments of equal length within a profile, appearing as a single band, which we call collision. The bias of D increases with larger numbers of bands, and lower genetic similarity. We propose two homoplasy- and collision-corrected estimators of genetic similarity. The first is a modification of D, replacing band counts by estimated fragment counts. The second is a maximum likelihood estimator, only applicable if band positions are available. Properties of the estimators are studied by simulation. Standard errors and confidence intervals for the first are obtained by bootstrapping, and for the second by likelihood theory. The estimators are nearly unbiased, and have for most practical cases smaller standard error than D. The likelihood-based estimator generally gives the highest precision. The relationship between fragment counts and precision is studied using simulation. The usual range of band counts (50–100) appears nearly optimal. The methodology is illustrated using data from a phylogenetic study on lettuce.

Introduction

AFLP is a DNA fingerprinting technique, that has been employed in many studies on plants (e.g. Tams et al. 2005), but also in studies on fungi (e.g. Mebrate et al. 2006), bacteria (e.g. Duim et al. 2001), and animals (e.g. Foulley et al. 2006). The resulting DNA fingerprints, also called profiles, are used in a wide spectrum of applications, like QTL studies (e.g. Zhong et al. 2006), diversity studies (e.g. van Berloo et al. 2008), and optimization of gene bank management (e.g. Jansen and van Hintum 2007). The question has been raised whether AFLP will remain useful in the near future, given the advances in genome sequencing, and new large-scale genotyping techniques like DArT (Wenzl et al. 2004). Meudt and Clarke (2007) suggest that fingerprinting techniques in general, and AFLP in particular, will remain valuable, especially if new analysis methods are developed, which overcome the problems arising in the analysis of AFLP data.

In this paper, we study the estimation of pairwise genetic similarity from dominant AFLP data. Estimation of similarity may be hampered by errors in, or erroneous interpretation of the binary band information from the AFLP profiles. As Bonin et al. (2007) mention, two types of errors prevail in AFLP genotyping: scoring errors and homoplasy. Many papers study the problem of scoring errors (e.g. parts of Meudt and Clarke 2007, and papers cited therein), but here we focus on homoplasy.

Estimation of genetic similarity is biased due to size homoplasy, see Fig. 1 (to be discussed later in greater detail). Size homoplasy occurs if, for two individuals, equally sized, but different DNA fragments comigrate in two AFLP lanes, resulting in identical bands. The two bands are usually considered homologous. Hence, part of the observed similarity can be attributed to chance. Size homoplasy is considered to be one of the major problems in the analysis of AFLP data (Meudt and Clarke 2007; Robinson and Harris 1999). Caballero et al. (2008) study the effect of size homoplasy on estimates of genetic diversity and detection of selective loci. Empirical estimates of the amount of homoplasy can be found, e.g. in O’Hanlon and Peakall (2000), who report that among congeneric thistles comigrating fragments showed on average 2.5% size homoplasy, but among different subtribes up to 100%. Because of this problem, AFLP is commonly advised to be used only to assess relationships of closely related taxa (Althoff et al. 2007).

Fig. 1

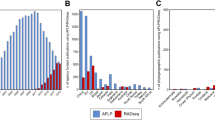
a Average Dice, and b average Jaccard similarities as a function of number of fragments for 100,000 simulated pairs of profiles with genetic similarities p_gs = 0.0, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95. Fragments are sampled from fld F_S with scoring range 51–500. The top axes show the average number of bands on a non-linear scale

Another problem, related to the size homoplasy mentioned above, is the occurrence of two or more equally sized, but different fragments within a single lane. As two equally sized different fragments in two lanes generally comigrate, and are wrongly interpreted as homologous, they will also comigrate if amplified within a single lane, colliding in a single band, and wrongly interpreted as single fragment. We call the comigration of equally sized fragments within a single lane collision. In an empirical study on sugarbeet, Hansen et al. (1999) quantified the problem. They found 13.2% of the bands to contain collisions. In an in silico study of AFLP for a wide variety of species, Althoff et al. (2007) found fractions of bands containing collisions up to 49%, depending on the number of bands in a lane. Vekemans et al. (2002) reported in a Monte Carlo simulation study an average percentage of 30% of undetectable fragments. Collisions were studied from a probabilistic point of view in Gort et al. (2006) and Gort et al. (2008). Their theoretical results, which are at the basis of the present paper, are in line with the empirical results given above. Collisions also affect the estimation of genetic similarity.

Although it is recognized that both size homoplasy and collision may occur in AFLP, no attempts are usually made to correct for the problems: two equally sized bands are considered homologous, and a single band is interpreted as a single fragment. The reasons for this negligence are at least twofold: it is felt that the problems are minor (in the cases where AFLPs are suggested to be used), and hardly any methodology exists to correct for it. In Koopman and Gort (2004) a crude approach was proposed for the calculation of similarities from AFLP profiles.

In the present paper new estimators of genetic similarity from AFLP bands, corrected for homoplasy and collision, are proposed, one based on modification of the Dice and Jaccard coefficients, and one based on maximum likelihood. We take the following steps in the “Materials and methods” part to arrive at these estimators.

• We first review the AFLP procedure as a sampling method of DNA fragments.

• Next, the procedure and data are described from a modeling point of view, introducing notation, and a definition of pairwise genetic similarity for binary AFLP data is given.

• We review some commonly used similarity coefficients.

• We demonstrate, by simulation, that homoplasy and collision may seriously bias similarity estimates, resulting in Fig. 1.

• A first step towards a solution is to estimate the number of fragments in a lane from the number of bands. We describe two ways to do this, depending on the availability of band position information.

• Using estimated fragment counts, modified Dice (and Jaccard) coefficients in two versions are proposed, depending on availability of band position information.

• If band position information is available, a second estimator of genetic similarity is proposed, based on maximum likelihood (m.l.).

• Standard errors and confidence intervals are obtained, using the bootstrap for the modified coefficients, and standard likelihood theory for the m.l. estimator.

• Further distributional characteristics of the estimators are studied by simulation. We describe precisely how we sample AFLP profiles.

Using the m.l. estimator and its precision, we next focus on the question how many bands in a lane should be used to estimate genetic similarity optimally. The theory is illustrated by a small case study on lettuce, using data from a phylogenetic study by Koopman et al. (2001). Results of the simulations and the case study are shown in “Results”. Conclusions are compiled and discussed in “Conclusions and discussion”. The paper ends with appendices on bootstrapping and an overview of all symbols used.

Materials and methods

AFLP reviewed

To understand the ideas we are proposing, a short review of the AFLP fingerprinting technique is useful. The AFLP technique, developed by Keygene N. V. (Vos et al. 1995), can be looked upon as a sampling technique of DNA fragments from, hopefully, random locations within a genome. To arrive at a sample of DNA fragments representing an individual genome four steps are taken:

• 1. The total genomic DNA is cut into fragments by two restriction enzymes, often MseI (“frequent cutter”) and EcoRI (“rare cutter”). The result is a soup of fragments, flanked with restricted EcoRI–EcoRI, EcoRI–MseI, or MseI–MseI sites.

• 2. Two adaptors, specific for the restriction enzymes, are ligated to the fragments, allowing primers to adhere in the third step.

• 3. Two primers, complementary to the two adaptors, with one or more selective nucleotides select a number of fragments for PCR amplification. In this way a sample of fragments is drawn. Primers with more selective nucleotides will select fewer fragments. If the four nucleotides A–C–T–G occur equally often in the genome, one extra selective nucleotide on, e.g. the EcoRI primer will cause a fourfold reduction in sample size of EcoRI–MseI fragments, and a 16-fold reduction of the EcoRI–EcoRI fragments.

• 4. The amplified fragments are separated by length in a lane of a gel or capillary electrophoresis system. Shorter fragments travel further. Usually only fragments with at least one EcoRI primer are labeled, and will become visible as bands. Only fragments with lengths within a certain scoring range (e.g. 51–500 nucleotides long) are visualized as bands.

On a single gel multiple individual genomes are fingerprinted, one per lane. The lengths of the bands are determined by comparison with the position of DNA fragments of known lengths (sizers) in size ladders. For a complete review of the AFLP technique, see e.g. Mueller and LaReesa Wolfenbarger (1999).

AFLP modeled: single profile

In this section, we again step through the AFLP procedure, but now aim to statistically model the procedure and data. For convenience, we compile all introduced symbols in Appendix 2 (Table 7). We describe the procedure for a single lane of a gel.

In the first two steps of the procedure, the total genomic DNA is cut into fragments, and adaptors are ligated. Only part of these fragments are eligible for visualization: fragments containing at least one labeled site (e.g. Eco-RI site), and within the used scoring range (e.g. with 51–500 nucleotides) are candidates. We call this subset the population of fragments Π, containing, say, M fragments. Different restriction enzymes will result in different populations of fragments. The size and nucleotide composition of the genome also affect Π.

The length of a fragment is the number of nucleotides, adaptors included. We label the possible lengths of the fragments in Π with index i, ranging from 1 (referring to the smallest length in the scoring range) to N (referring to the largest length; e.g. with scoring range 51–500 N = 450). The probability distribution of the lengths is called the fragment length distribution (fld). With p _i the probability that a fragment, randomly drawn from Π, has length i, we can write fld = (p ₁, p ₂,…, p _N ); note that $\sum\nolimits_{i = 1}^{N} {p_{i} = 1}.$ Shorter fragments are more frequent than longer fragments, i.e. the fld is monotonically decreasing and skewed to the right (Gort et al. 2006). The amount of skewness is mainly determined by the GC content of the genome, if the frequent cutter MseI is used. Lower GC content results in shorter fragments.

We assume the fld is known, or, at least, there is a reliable estimate of it. For all simulations we use fld F _S, estimated from the Arabidopsis thaliana genome based on in silico AFLP, as in Gort et al. (2006). This fld is reasonable for genomes with GC content close to 36%. For the estimation of the fld for other genomes we refer to the same publication.

In step 3 the primers select a sample of fragments from Π, selecting only those fragments, which have specific nucleotides next to the restriction sites. This resembles systematic sampling, but with unknown sample size. We treat the lengths of the sampled fragments as a random sample from fld. Assuming a constant but unknown sampling probability π for the fragments of Π, the number of fragments in the sample, called k, has approximately a Poisson distribution with expected count m = πM.

In step 4 the k fragments are separated by length, and visualized as bands. We assume that the position of a band within a lane is determined principally by the fragment length. Hence, a band will occur approximately at one of N discrete positions within a lane, which we call band lengths. A consequence is that two different fragments of the same length will occur as a single band.

The end product is a profile, containing bands at discrete positions, which can be represented by a binary vector y = (y ₁, y ₂,…, y _N ). The binary variable y _i (i = 1,…, N) indicates whether a band with length i is present. The number of bands in a lane is $n = \sum\nolimits_{i = 1}^{N} {y_{i} }.$ Notice that the number of bands cannot be larger than the number of fragments (n ≤ k).

AFLP modeled: pairs of profiles and their similarity

Two related individuals share parts of their DNA. As a consequence, they share part of their two populations of fragments Π₁ and Π₂, containing M ₁ and M ₂ fragments, formed at step 2. This common part is called Π _a , and contains M _a fragments. The complement of Π _a within Π₁ is called Π _b , consisting of M _b fragments present in individual 1, but absent in 2. The complement of Π _a within Π₂ is called Π _c , and consists of M _c fragments, present in 2, but absent in 1. Π _b and Π _c are called the populations of unique fragments. Notice that M ₁ = M _a  + M _b , and M ₂ = M _a  + M _c . All population sizes M _a , M _b , and M _c are unknown. The fractions of common fragments are F ₁ = M _a /M ₁ and F ₂ = M _a /M ₂, which need not be the same, e.g. if the genomes have different sizes.

We define the pairwise genetic similarity p _gs of a pair of genotypes as the weighted average of fractions F ₁ and F ₂, with weights proportional to the population sizes:

$$ p_{\text{gs}} = \frac{{M_{1} }}{{M_{1} + M_{2} }}F_{1} + \frac{{M_{2} }}{{M_{1} + M_{2} }}F_{2} = w_{1} F_{1} + w_{2} F_{2} $$

(1)

Notice that p _gs can be written as 2 M _a /(2 M _a  + M _b  + M _c ).

We assume that Π _a , Π _b , and Π _c have the same fragment length distribution fld.

In step 3 samples from fld are taken, resulting in sample sizes of fragments k _a , k _b , and k _c , approximately Poisson distributed with expected fragment counts m _a , m _b , and m _c , proportional to M _a , M _b , and M _c . The expected numbers of fragments of the two profiles are m ₁ = m _a  + m _b and m ₂ = m _a  + m _c .

The end product after step 4 is a pair of profiles, represented by two binary band vectors y ₁ = (y ₁₁,…, y _N1), and y ₂ = (y ₁₂,…, y _N2), with band counts $n_{j} = \sum\nolimits_{i = 1}^{N} {y_{ij} }$ (j = 1, 2). We use the following notation for band counts:

• a = number of shared bands in the two profiles = $\sum\nolimits_{i = 1}^{N} {y_{i1} y_{i2} }$;

• b = number of bands in the first profile, but absent in the second = $\sum\nolimits_{i = 1}^{N} {y_{i1} \left( {1 - y_{i2} } \right)}$;

• c = number of bands in the second profile, but absent in the first =$\sum\nolimits_{i = 1}^{N} {\left( {1 - y_{i1} } \right)} y_{i2}$;

• d = number of empty positions in both profiles = $\sum\nolimits_{i = 1}^{N} {\left( {1 - y_{i1} } \right)} \left( {1 - y_{i2} } \right)$.

Hence, a, b, c and d are the number of 1–1, 1–0, 0–1, and 0–0 matches, respectively. If more than two profiles are compared, d is often defined as the number of 0–0 matches in two lanes, limited to those band lengths with at least one band in one of the other lanes.

Commonly used similarity coefficients

We now review some commonly used similarity coefficients for binary AFLP data. From the similarity coefficients, reviewed by Reif et al. (2005), only the Dice, Jaccard’s, and simple matching coefficient are relevant, because we treat AFLP as a dominant marker system.

The Dice coefficient (Dice 1945) D is an estimator of p _gs: $D = \frac{2a}{2a + b + c} = \hat{w}_{1} \hat{F}_{1} + \hat{w}_{2} \hat{F}_{2}$ with weights $\hat{w}_{1} = \tfrac{{n_{1} }}{{n_{1} + n_{2} }}$, $\hat{w}_{2} = \tfrac{{n_{2} }}{{n_{1} + n_{2} }}$, and $\hat{F}_{1} = \tfrac{a}{{n_{1} }}$, $\hat{F}_{2} = \tfrac{a}{{n_{2} }}$. In genetic contexts the Dice similarity is often referred to as the Nei–Li similarity (Nei and Li 1979).

The Jaccard coefficient (Jaccard 1908) $J = \frac{a}{a + b + c}$ is the fraction of common bands compared to the total number of different bands for the two profiles. It is an estimator of M _a /(M _a  + M _b  + M _c ), and not of the genetic similarity, as we define it. A non-linear relationship exists between J and D: $J = \frac{D}{2 - D}$. For example, taking equal band counts in the two profiles: if half of the bands in each profile is shared, then D = 1/2, and J = 1/3. Examples of applications of Dice and Jaccard’s coefficients as measures of genetic similarity are Drossou et al. (2004), and Tams et al. (2005).

The simple matching coefficient (Sneath and Sokal 1973) $S = \frac{a + d}{a + b + c + d}$ measures similarity including the 0–0 matches in the profiles as well, counting the 1–1 and 0–0 matches alike.

To illustrate the differences between the coefficients, take two genotypes with profiles containing 100 bands each, with N = 450, a = 50, b = 50, c = 50, hence d = 300. Since half of the bands of each profile is shared, D = 0.5, and J = 0.33, whereas S = 0.78. Suppose that for the same genotypes a second set of profiles is made, using primers with more selective nucleotides, and hence smaller samples of amplified fragments. Assuming a proportional decrease of band counts of 50% (so a = 25, b = 25, c = 25, and d = 375), we still have D = 0.5, and J = 0.33, but S = 0.89. Hence, S changes if the band counts decrease proportionally, whereas D and J remain constant.

Usually more than two genotypes are compared in a study. Often, for S only the 0–0 matches are counted for the occupied band positions in the whole set of genotypes. With a proportional decrease of the band counts a, b and c, the null count d will also decrease, but likely at a different rate. Hence, S will likely change, whereas D and J remain constant. S can also change if the set of other genotypes under study is changed. Wong et al. (2001) supply reasons in the realm of codominance of AFLP to avoid similarity measures exploiting 0–0 matches. Therefore, S has a number of undesirable properties. Only D is an estimator of pairwise genetic similarity, as we have defined it.

The problem: homoplasy and collision

To appreciate the possible consequences of homoplasy and collisions in relationship studies based on AFLP data, we performed a simulation study. We sampled 100,000 pairs of profiles for a range of genetic similarities p _gs (=0, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95) and fragment counts m ₁ = m ₂ (=1,…, 200). The maximum fragment count m = 200 corresponds to ≈140 bands, which is about the maximum number of bands per lane to be found in practice. Each pair was sampled in three steps. First, a random draw k _a from the binomial (m ₁, p _gs) distribution determined the sample size of fragments from the common part Π _a , the remaining k _b  = m ₁ − k _a and k _c  = m ₂ − k _a fragments to be sampled from the unique parts Π _b and Π _c . Next, k _a , k _b , and k _c lengths were sampled from the fld, and results were combined into two vectors of length N = 450, containing the counts of lengths 1,…, 450 for the two profiles. In the last step, a pair of binary vectors was created, containing absence/presence information of at least one fragment of length 1,…, 450, and representing a pair of AFLP profiles. Dice and Jaccard coefficients D and J were calculated for each pair, and averaged over all pairs to produce Fig. 1. The graph shows the average D and J as a function of the fragment count. The average band count is shown at the top axis on a non-linear scale. As an example, profiles with 100 fragments tend to produce approximately 83 bands, hence 17 collisions.

D overestimates the true genetic similarity seriously, increasingly so for larger fragment or band counts, and for smaller genetic similarities. For example, at band count 60 the average D has approximate biases 0.015, 0.085, and 0.23 for p_gs = 0.9, 0.5, and 0.0, respectively. At band count 100 the biases are 0.025, 0.14 and 0.34, respectively.

J is for band counts in the range 60,…, 100 sometimes lower than the true p_gs (if p_gs > 0.3), sometimes close to p_gs (if p_gs ≈ 0.3) and sometimes higher (if p_gs < 0.3).

Estimation of number of fragments

The basic idea in this paper is that, in order to estimate genetic similarity, we need to know how many fragments from the two profiles are identical, whereas the profiles indicate how many bands are identical. The first step to solve this problem is to estimate the expected number of fragments m that gave rise to the n observed bands in a single profile. The difference between number of fragments and number of bands is called the collision count.

To estimate m, we discriminate between situations without and with band length information. Notice that band lengths are not always available, although in principle the information can be read from an AFLP gel, if size ladders are used. The lack of band length information is often based on limitations in the realm of intellectual property, as commercial players like Keygene N.V. propagate.

In the case of unknown band lengths, the collision count for a given fld is estimated from the band count, using Bayes’ rule and generalized occupancy distributions, see Gort et al. (2006). The resulting estimator of the expected number of fragments m is called $\hat{m}_{{\bar{L}}}$.

With known band lengths, the number of collisions can be estimated using Bayes’ rule and approximated multinomial tail probabilities, or applying the EM-algorithm, as in Gort et al. (2008). In the present paper, we report a simpler approach to arrive at an estimator of m. We propose a generalized linear model (g.l.m.) (McCullagh and Nelder 1991) for the binary band scores y _i . The scores y _i are assumed to be independent, and Bernoulli (P _i ) distributed, with expected score E(y _i ) = P _i the probability that a band occurs with length i, if a sample of m fragments has been drawn from fld= $\left( {p_{1} , \ldots, p_{N} } \right)$. The band probability P _i and fragment probability p _i are related as: $\left( {1 - P_{i} } \right) = \left( {1 - p_{i} } \right)^{m}$, because the event “no band of length i” is equivalent with “none of the m fragments has length i”. This equation can be transformed into

$$ {\rm log} \left( { - {\rm log} \left( {1 - P_{i} } \right)} \right) = {\rm log} \left( m \right) + {\rm log} \left( { - {\rm log} \left( {1 - p_{i} } \right)} \right), $$

revealing the systematic part of the g.l.m. Hence, we fit a regression model for the band scores y _i , using log(m) as intercept, offset ${\rm log}\left( { - {\rm log}\left( {1 - p_{i} } \right)} \right)$, and complementary log–log link. The estimator $\hat{m}_{L}$ of m is obtained by exponentiation of the estimator of the intercept log(m).

Modified Dice and Jaccard coefficients using binary AFLP data

Suppose we have two profiles with observed band counts n ₁ = a + b, and n ₂ = a + c. The expected numbers of fragments m ₁ and m ₂ are estimated by $\hat{m}_{1}$ and $\hat{m}_{2}$ by either of the two estimators from the previous section. The pairwise genetic similarity to be estimated is $p_{\text{gs}} = \frac{{M_{1} }}{{M_{1} + M_{2} }}\,\frac{{M_{a} }}{{M_{1} }} + \frac{{M_{2} }}{{M_{1} + M_{2} }}\,\frac{{M_{a} }}{{M_{2} }} = w_{1} F_{1} + w_{2} F_{2}$, as in (1).

For weights w ₁ and w ₂, we have straightforward estimators $\hat{w}_{1} = \tfrac{{\hat{m}_{1} }}{{\hat{m}_{1} + \hat{m}_{2} }}$, and $\hat{w}_{2} = \tfrac{{\hat{m}_{2} }}{{\hat{m}_{1} + \hat{m}_{2} }}$, since expected fragments counts are assumed to be proportional to population sizes. However, for the fractions common fragments $F_{1} = \tfrac{{M_{a} }}{{M_{1} }}$ and $F_{2} = \tfrac{{M_{a} }}{{M_{2} }}$, an estimator $\hat{m}_{a}$ of the number of common fragments m _a is needed. We estimate m _a as $\hat{m}_{a} = \hat{m}_{1} + \hat{m}_{2} - \hat{m}_{1 + 2}$, by analogy with the number of shared bands a, which can be calculated as a = n ₁ + n ₂ − n ₁₊₂. In this formula n ₁₊₂ = a + b + c is the total number of different bands, as if combining the two profiles into a single profile, and counting the bands. In the formula for $\hat{m}_{a}$, $\hat{m}_{1 + 2}$ is the estimated fragment count for the combination of the two profiles. The rationale of estimator $\hat{m}_{a}$ is the following: $\hat{m}_{1}$ estimates the number of fragments from the n ₁ bands of profile 1, and $\hat{m}_{2}$ from the n ₂ bands of profile 2. The sum $\hat{m}_{1} + \hat{m}_{2}$ estimates the total number of fragments in the two lanes. Some of the fragments are counted twice, as they occur in both profiles. If we overlay profiles 1 and 2, we see what would have happened if we mixed the populations of fragments for the two genomes, and made a profile for the mixture. Identical fragments in the two populations, selected for amplification, will appear as a single band now, and $\hat{m}_{1 + 2}$ estimates the total number of fragments in the profile for the mixture, that is the number of different fragments in the mixture. Then the difference ($\hat{m}_{1} + \hat{m}_{2}$) – $\hat{m}_{1 + 2}$ estimates $\hat{m}_{a}$, i.e. the number of fragments the two profiles have in common.

This results in $\hat{F}_{1} = \tfrac{{\hat{m}_{a} }}{{\hat{m}_{1} }}$ and $\hat{F}_{2} = \tfrac{{\hat{m}_{a} }}{{\hat{m}_{2} }}$. Estimators of unique fragment counts are $\hat{m}_{b} = \hat{m}_{1} - \hat{m}_{a}$, and $\hat{m}_{c} = \hat{m}_{2} - \hat{m}_{a}$.

As estimator of genetic similarity p _gs we now propose the modified Dice coefficient

$$ D^{\rm mod } = \frac{{\hat{m}_{1} }}{{\hat{m}_{1} + \hat{m}_{2} }}\frac{{\hat{m}_{a} }}{{\hat{m}_{1} }} + \frac{{\hat{m}_{2} }}{{\hat{m}_{1} + \hat{m}_{2} }}\frac{{\hat{m}_{a} }}{{\hat{m}_{2} }} = \frac{{2\hat{m}_{a} }}{{2\hat{m}_{a} + \hat{m}_{b} + \hat{m}_{c} }}, $$

replacing the band counts in the original Dice coefficient by estimated fragment counts. The Jaccard coefficient may be modified in the same way:

$$ J^{\rm mod} = \hat{m}_{a} /\left( {\hat{m}_{a} + \hat{m}_{b} + \hat{m}_{c} } \right) $$

The maximum of both D ^mod and J ^mod is 1, occurring if the two profiles are identical. At the other end of the scale, there is no intrinsic limitation both for D ^mod and J ^mod to take on negative values, whereas p _gs ≥ 0. A solution to the problem is truncation of the estimator at 0.

The modified coefficients come in two versions, for situations without and with band length information. If band lengths are unknown, estimator $\hat{m}_{{\bar{L}}}$ is used, resulting in modified Dice and Jaccard coefficients

$$ D_{{\bar{L}}}^{\rm mod} = 2\hat{m}_{{\bar{L}a}} /\left( {2\hat{m}_{{\bar{L}a}} + \hat{m}_{{\bar{L}b}} + \hat{m}_{{\bar{L}c}} } \right),{\text{ and }}J_{{\bar{L}}}^{\rm mod} = \hat{m}_{{\bar{L}a}} /\left( {\hat{m}_{{\bar{L}a}} + \hat{m}_{{\bar{L}b}} + \hat{m}_{{\bar{L}c}} } \right) $$

If band lengths are known, we use estimator $\hat{m}_{L}$, and the modified coefficients become

$$ D_{L}^{\rm mod} = 2\hat{m}_{La} /\left( {2\hat{m}_{La} + \hat{m}_{Lb} + \hat{m}_{Lc} } \right)\,,{\text{ and }}J_{L}^{\rm mod} = \hat{m}_{La} /\left( {\hat{m}_{La} + \hat{m}_{Lb} + \hat{m}_{Lc} } \right) $$

Maximum likelihood estimator of genetic similarity from binary AFLP data

In the case of known band lengths, a second estimator $D^{\text{\rm mle}}$ of the genetic similarity p _gs is proposed, based on maximum likelihood (m.l.) (Silvey 1975). For this estimator we need a statistical model for the data, consisting of the N pairs of binary scores $\left( {y_{11} ,y_{12} } \right)$, $\left( {y_{21} ,y_{22} } \right), \ldots ,\left( {y_{N1} ,y_{N2} } \right).$ We treat these pairs as independent. The two profiles have expected fragment counts $m_{1} = m_{a} + m_{b}\;{\text{and}}\;m_{2} = m_{a} + m_{c} ,$ as before.

The four possible outcomes of a pair $\left( {y_{i1} ,y_{i2} } \right)$ are:

• 1. (0,0): no fragment of length i at all;

• 2. (0,1): no fragment from the unique part Π _b of genotype 1 and the common part Π _a , and at least one fragment from the unique part Π _c of genotype 2;

• 3. (1,0): at least one fragment from Π _b , and no fragment from Π _c and Π _a ;

• 4. (1,1): either at least one fragment from Π _a , or at least one fragment from both Π _b and Π _c , but not from Π _a .

The likelihood of these four outcomes for the ith pair is:

• 1. (0,0): $\ell_{i} = \left( {1 - p_{i} } \right)^{{m_{b} + m_{a} + m_{c} }}$

• 2. (0,1): $\ell_{i} = \left( {1 - p_{i} } \right)^{{m_{b} + m_{a} }} \left( {1 - \left( {1 - p_{i} } \right)^{{m_{c} }} } \right)$

• 3. (1,0): $\ell_{i} = \left( {1 - \left( {1 - p_{i} } \right)^{{m_{b} }} } \right)\left( {1 - p_{i} } \right)^{{m_{a} + m_{c} }}$

• 4. (1,1): $\ell_{i} = \left( {1 - \left( {1 - p_{i} } \right)^{{m_{a} }} } \right) + \left( {1 - \left( {1 - p_{i} } \right)^{{m_{b} }} } \right)\left( {1 - p_{i} } \right)^{{m_{a} }} \left( {1 - \left( {1 - p_{i} } \right)^{{m_{c} }} } \right)$

Next, the log-likelihood of the data ${\text{LL}} = \sum\nolimits_{i = 1}^{N} {{\rm log}\left( {\ell_{i} } \right)}$ is maximized with respect to the parameters m _a , m _b , and m _c , resulting in m.l. estimators $\hat{m}_{a}$, $\hat{m}_{b}$, and $\hat{m}_{c}$. As in the previous section, we can define a modified Dice coefficient, now based on m.l. estimators, as

$$ D_{ 1}^{\text{mle}} = \frac{{2\hat{m}_{a} }}{{2\hat{m}_{a} + \hat{m}_{b} + \hat{m}_{c} }} = \hat{w}_{1} \hat{p}_{1} + \hat{w}_{2} \hat{p}_{2} $$

with weights $\hat{w}_{1} = \tfrac{{\hat{m}_{a} + \hat{m}_{b} }}{{\hat{m}_{a} + \hat{m}_{b} + \hat{m}_{a} + \hat{m}_{c} }}$, $\hat{w}_{2} = \tfrac{{\hat{m}_{a} + \hat{m}_{c} }}{{\hat{m}_{a} + \hat{m}_{b} + \hat{m}_{a} + \hat{m}_{c} }}$, and $\hat{p}_{1} = \tfrac{{\hat{m}_{a} }}{{\hat{m}_{a} + \hat{m}_{b} }}$, $\hat{p}_{2} = \tfrac{{\hat{m}_{a} }}{{\hat{m}_{a} + \hat{m}_{c} }}$.

The m.l. procedure returns approximate standard errors of $\hat{m}_{a}$, $\hat{m}_{b}$, and $\hat{m}_{c}$, but not of $D_{ 1}^{\text{mle}}$ as an estimator of p _gs. To get the precision of an estimator of p _gs, we reparameterize the likelihood. From $p_{\text{gs}} = \tfrac{{2M_{a} }}{{2M_{a} + M_{b} + M_{c} }}$, it follows $\tfrac{{p_{\text{gs}} }}{{1 - p_{\text{gs}} }} = \tfrac{{M_{a} }}{{\left( {M_{b} + M_{c} } \right)/2}} = \tfrac{{m_{a} }}{{\left( {m_{b} + m_{c} } \right)/2}}$, since we assume expected fragment counts proportional to population counts. Now, we replace m _a in the likelihood above by $\tfrac{{p_{\text{gs}} }}{{1 - p_{\text{gs}} }}\left( {m_{b} + m_{c} } \right)/2$. Now the log-likelihood is maximized with respect to p _gs, m _b , and m _c , resulting in a direct m.l. estimator of p _gs, which we call $D_{2}^{\text{mle}}$.

A third parameterization replaces m _a by $\tfrac{1}{2}\left( {m_{b} + m_{c} } \right){ \exp }\left( {l_{\text{gs}} } \right)$, with l _gs = logit(p _gs), yielding an estimator on the logit-scale, to be back-transformed to $D_{ 3}^{\text{mle}}\, {\text{logit}}^{-1}\left( {\hat{l}_{\text{gs}} } \right)= { \exp }\left( {\hat{l}_{\text{gs}} } \right) /\left({1+ \exp }\left( {\hat{l}_{\text{gs}} } \right)\right)$. This estimator may have better distributional properties for p _gs close to 0 or 1.

Precision of the estimators

The precisions of estimators $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$ are determined by bootstrapping (Efron and Tibshirani 1993), whereas for $D^{\text{mle}}$ the precision follows from standard likelihood theory.

For estimator $D_{{\bar{L}}}^{\rm mod}$ the following bootstrap method is used. The data for a pair of profiles consists of a pairs 1–1, b pairs 1–0, c pairs 0–1, and d pairs 0–0, collected in the vector (a, b, c, d), without knowledge of band lengths. For one bootstrap resample we take a sample of size N from the pairs 1–1, 1–0, 0–1, and 0–0, with probabilities given by a/N, b/N, c/N, and d/N, respectively. For this bootstrap sample the modified Dice coefficient is calculated as described, and stored.

For estimator $D_{L}^{\rm mod}$ a different bootstrap method is used. Now the band lengths are known. A bootstrap resample consists of a sample with replacement of N pairs $\left( {y_{i1} ,y_{i2} } \right)$ and connected fld probabilities p _i from the N pairs $\left( {y_{11} ,y_{12} } \right)$, $\left( {y_{21} ,y_{22} } \right), \ldots ,\left( {y_{N1} ,y_{N2} } \right),$ and a rescaling of the set of p _i ’s to have sum 1. Notice that the same pair $\left( {y_{i1} ,y_{i2} } \right)$, i.e. with the same band length, may occur more than once in the bootstrap resample. Therefore, a single bootstrap resample does not necessarily correspond to a pair of profiles, which could occur in practice. The method nevertheless works well, as shown later.

For $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$ we took 1,000 bootstrap samples, resulting in estimates of bias (defined as bootstrap mean − estimate), standard error, and bootstrap confidence intervals. We used accelerated bias-corrected percentile bootstrap confidence intervals, also known as BC _a confidence intervals (DiCiccio and Efron 1996). For a description of the calculation of these confidence intervals, as well as a comparison between different types of bootstrap confidence intervals, we refer to the appendix.

For estimator $D_{ 2}^{\text{mle}}$ approximate standard errors follow from standard likelihood theory, leading to Wald confidence intervals for p _gs as $D_{ 2}^{\text{mle}} \pm {\rm SE}\left( {D_{ 2}^{\text{mle}} } \right)z_{1 - \alpha /2}$, with z _1-α/2 the 1 − α/2 quantile from the standard normal distribution. For $D_{3}^{\text{mle}}$ we back-transform the Wald-confidence interval ${\hat{l}_{\text{gs}} } \pm {{\rm SE}} \left({\hat{l}_{\text{gs}} }\right) {\cdot} {z_{1 - \alpha /2}}$ using ${\text{logit}}^{-1}$. Besides Wald-type confidence intervals we calculated profile likelihood confidence intervals for p _gs (see e.g. Venzon and Moolgavkar 1988). For profile likelihood confidence intervals the parameters m _b and m _c are treated as nuisance parameters, resulting in a profile likelihood for p _gs by maximizing over m _b and m _c .

Sampling of AFLPs and simulation

To study the behavior of the proposed estimators, we performed a simulation study. For a wide range of parameter settings (p _gs, m ₁, and m ₂) pairs of profiles were simulated by

• 1. calculating the expected counts of common fragments m _a  = ½(m ₁ + m ₂)p _gs, and unique fragments m _b  = m ₁ − m _a , and m _c  = m ₂ − m _a ;

• 2. drawing random counts from Poisson distributions with means m _a , m _b , and m _c to arrive at fragment counts k _a , k _b , and k _c for the pair of profiles to be generated;

• 3. sampling separately k _a , k _b , and k _c fragment lengths from the fld;

• 4. combining the k _a  + k _b sampled fragments into the first profile, and k _a  + k _c fragments into the second, condensing the information into binary vectors y ₁ and y ₂ of length N.

For all combinations of p _gs = (0, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95) and m ₁ = m ₂ = (40, 70, 120), we sampled 10,000 pairs of profiles. We also included a selection of unequal m’s for some values of p _gs, to show that the methodology works in that case as well. For each pair of profiles the estimates $D_{{\bar{L}}}^{\rm mod}$, $D_{L}^{\rm mod}$ (with 1,000 bootstrap samples), and the three versions of $D^{\text{mle}}$ were calculated.

Application of methodology: effect of number of fragments on precision

In AFLP profiling the number of fragments in a lane, and hence the number of bands, can be steered by the researcher by changing the number and/or type of selective nucleotides of the primers. Typical band counts per lane are between 50 and 100, corresponding to fragment counts from 60 to 125. The question arises whether these typical counts are optimal, i.e. whether the estimators of genetic similarity have highest possible precision.

In a simulation study we investigated for a number of examples (as before, p _gs = 0.0, 0.1, 0.3, 0.5, 0.7, 0.9, and 0.95 using N = 450 and fld F _S ), how the standard error and width of the 95% profile likelihood confidence interval of p _gs based on $D_{2}^{\text{mle}}$ depends on the fragment count. Expected fragment counts were varied from 15 to 500 (in steps of 5, equal expected counts for pairs of profiles), using 10,000 replicates at each step. We pushed the number of fragments to unrealistically high values now, to show the properties of $D_{2}^{\text{mle}}$ in that case, at the same time realizing that in practice it is impossible to score profiles with very large numbers of bands per lane. In the simulations numbers of fragments up to 500 were allowed, resulting in profiles with more than 225 bands on average. In that case more than half of the band positions are occupied, since N = 450.

Case study: phylogenetic relations between Lactuca genera

The lettuce study by Koopman et al. (2001) aims at inferring species relationships in Lactuca and related genera from AFLP fingerprints. We selected one of the two primer combinations (E35/M49), and only 5 of the 20 species: L. tenerrima, M. muralis, L. serriola, L. sativa, and L. tatarica. We took 6–9 accessions for each of the five selected species. We selected the five species to have a wide range of band counts: mean counts (±SD) are 29.6 (±1.9), 32.4 (±2.5), 49.6 (±3.0), 52.6 (±2.8), and 84.1 (±5.1) for L. tenerrima, M. muralis, L. serriola, L. sativa, and L. tatarica, respectively.

For all pairs of accessions we calculated D, J, and D ^mle. We used F _S from A. thaliana as fld. This seems reasonable, since the GC content of lettuce is close to that of A. thaliana: 36.6, 37, 38.2, 38.3, and 36.4% for the five species (Koopman et al. 2002) versus 36% for A. thaliana. The relationships between the species are visualized with UPGMA dendrograms, using dissimilarities 1 − D, 1 − J, and 1 − D ^mle.

Results

General results from the simulation study

Table 1 shows some general results from the simulation study. For all simulation settings of p _gs, m ₁, and m ₂, the average band counts n ₁, n ₂, and average Dice similarity D are given. From the comparison of expected fragment counts with average band counts, we note that profiles with m = 40 have on average three collisions, with m = 70 on average 8.7 collisions, and with m = 120 on average 23.6 collisions. The ordinary Dice coefficient seriously overestimates the true similarity, with largest biases for small similarities and large fragment counts. The maximum observed bias is 0.334 for p _gs = 0 and m = 120. The smallest bias is 0.0034 for p _gs = 0.95 and m = 40.

Table 1 Average band counts n ₁ and n ₂, and Dice similarities D for 10,000 simulated pairs of AFLP profiles for a range of values of genetic similarity p _gs and expected numbers of fragments m ₁ and m ₂

Results from the simulation study for modified Dice coefficients

Table 2 shows the results from the simulation study for the modified Dice coefficient $D_{{\bar{L}}}^{\rm mod}$, using profiles without band length information. In Table 3 results for $D_{L}^{\rm mod}$ are given. We notice the following.

Table 2 Results from a simulation study on $D_{{\bar{L}}}^{\rm mod}$ for a range of values of genetic similarity p _gs and expected numbers of fragments m ₁ and m _2, 10,000 replicated pairs of AFLP profiles, 1,000 bootstrap resamples, fld F _S from A. thaliana with N = 450

Table 3 Results from a simulation study on $D_{L}^{\rm mod}$ for a range of values of genetic similarity p _gs and expected numbers of fragments m ₁ and m _2, 10,000 replicated pairs of AFLP profiles, 1,000 bootstrap resamples, fld F _S from A. thaliana with N = 450

• 1. Almost all of the bias of the original Dice coefficient is removed. $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$ slightly underestimate p _gs now (mean observed biases −0.0018 and −0.0015, averaged over all settings of p _gs and m, for $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$, respectively), with largest observed bias equal to −0.0030 occurring for $D_{{\bar{L}}}^{\rm mod}$ in case p _gs = 0 and m = 120. The remaining small negative bias can be removed even further by using a bootstrap bias correction. Mean observed biases are then −0.00058 and −0.00025.

• 2. The 95% (BC _a bootstrap) confidence intervals for the genetic similarity p _gs show reasonably good coverage properties. In 21 and 18 out of the 25 experimental settings the observed non-coverage is between 4.5 and 5.5%, hence deviations less than 0.5% from the nominal value of 5%. For both estimators the largest deviation from 5% is found for p _gs = 0.90 and m = 40, with observed non-coverages of 3.8 and 3.8%, respectively. In these cases the confidence intervals are slightly too wide. For p _gs = 0.95 and m = 40 the overall non-coverage behaves better (5.2 and 5.3%), but we find that in 1.6 and 1.7% of the cases the confidence intervals are too low, and in 3.6 and 3.5% too high, compared to the nominal 2.5 and 2.5%. In this case the intervals are too wide if the estimate is smaller than p _gs = 0.95, and too narrow for estimates larger than 0.95.

• 3. The bootstrap standard errors of $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$ are smaller for larger number of expected fragments, with the exception of p _gs = 0 and p _gs = 0.1. Hence, in the examples for p _gs > 0.1 larger fragment counts result in more precise estimates. The same can be said for the lengths of the 95% confidence intervals. If p _gs = 0.1 the smallest standard error is observed for m = 70

• 4. The estimates $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$ may become negative for small values of p _gs. In the table this can be seen for p _gs = 0, resulting in a negative average of D ^mod, but it also occurs for p _gs = 0.1. For p _gs = 0.3 the lower bound of the 95% confidence interval may become negative. In practice a negative value of D ^mod would be truncated at 0. Therefore, we added the bottom parts II of Tables 2 and 3, showing results for the truncated versions of $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$ for p _gs = 0.0, 0.1, and 0.3. Since the truncation causes more distributional asymmetry we give medians instead of averages of $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$. For $D_{{\bar{L}}}^{\rm mod}$ the bias-correction decreases the bias, but this is not always the case for $D_{L}^{\rm mod}$. For p _gs = 0 we give the non-coverage of the (97.5%) confidence interval only at the right of p _g = 0. For p _gs = 0 we observe the largest standard errors for the cases with largest m, suggesting that the optimal number of fragments is smaller than m = 120.

• 5. In all cases $D_{{\bar{L}}}^{\rm mod}$ has narrower 95% confidence intervals than $D_{L}^{\rm mod}$, although differences are small (average difference in length is only 0.0019). In all cases the bootstrap SE($D_{{\bar{L}}}^{\rm mod}$) ≤ SE($D_{L}^{\rm mod}$), but again differences are small. The coverage of the 95% confidence interval of $D_{{\bar{L}}}^{\rm mod}$ is slightly better than that of $D_{L}^{\rm mod}$: average absolute deviation from the nominal 5% is 0.33% for $D_{{\bar{L}}}^{\rm mod}$ compared to 0.36% for $D_{L}^{\rm mod}$. Intuitively better behavior of $D_{L}^{\rm mod}$ was expected, since $D_{L}^{\rm mod}$ exploits band length information, but we conclude, surprisingly, that $D_{{\bar{L}}}^{\rm mod}$ has slightly better characteristics than $D_{L}^{\rm mod}$

Results from the simulation study for maximum likelihood estimators D ^mle

Table 4 shows the results from the simulation study for $D^{\rm mle}$. We notice the following.

Table 4 Results from a simulation study on $D^{\rm mle}$ for a range of values of genetic similarity p _gs and expected numbers of fragments m ₁ and m _2, 10,000 replicated pairs of AFLP profiles, 1,000 bootstrap resamples, fld F _S from A. thaliana with N = 450

Table 5 Comparison of bootstrap confidence intervals for p _gs from a simulation study on $D_{{\bar{L}}}^{\rm mod}$ for a range of values of genetic similarity p _gs and expected numbers of fragments m ₁ and m _2, 10,000 replicated pairs of AFLP profiles, 1,000 bootstrap resamples, fld F _S from A. thaliana with N = 450

Table 6 Comparison of bootstrap confidence intervals for p _gs from a simulation study on $D_{L}^{\rm mod}$ for a range of values of genetic similarity p _gs and expected numbers of fragments m ₁ and m _2, 10,000 replicated pairs of AFLP profiles, 1,000 bootstrap resamples, fld F _S from A. thaliana with N = 450

• 1. Estimators $D_{1}^{\rm mle}$, $D_{2}^{\rm mle}$, and $D_{3}^{\rm mle}$ almost always return the same estimate. Only for p _gs ≥ 0.9 we see minor differences, resulting in means differing in the fourth decimal. Hence, only results for $D_{2}^{\rm mle}$ are shown.

• 2. The large positive bias of the original Dice coefficient is removed. For p _gs > 0.1, a negligible negative bias of $D_{2}^{\rm mle}$ remains: the mean bias is −0.0015. For p _gs ≤ 0.1 a small positive bias is observed, because of the necessarily non-negative value of the estimators. For p _gs = 0 the medians (not shown) are 0, and for p _gs = 0.1 they are 0.0965 (m = 40), 0.0982 (m = 70), and 0.0995 (m = 120).

• 3. The 95% Wald confidence intervals for p _gs are conservative for small values of p _gs (non-coverage rates smaller than nominal value), but are becoming more and more liberal for larger values. Obviously, the approximate standard error of $D_{2}^{\rm mle}$ is too large for small values of $D_{2}^{\rm mle}$, and too small for large values. The deviations from 5% seem acceptable for 0.3 ≤ p _gs ≤ 0.7 and m > 40. The number of intervals with a lower bound larger than the true p _gs outnumber those with an upper bound smaller than p _gs. This is also an indication of standard errors which are too high for low values of the estimate, and too small for large values.

• 4. The 95% profile likelihood confidence intervals for p _gs have for a large number of settings non-coverage rates close to 5%. In 16 out of the 25 settings the deviation of the non-coverage rate from the nominal value is less than 0.5%. Larger deviations are found for larger values of p _gs and smaller fragment counts. The largest deviation is observed for p _gs = 0.95 and m = 40, with a non-coverage rate equal to 19%, making the profile likelihood interval useless in this situation. The number of intervals with an upper bound smaller than p _gs becomes exceedingly large in these cases. The profile likelihood intervals work well for p _gs < 0.7, irrespective of the studied fragment counts, and for larger values of p _gs, but only if the fragment count is large enough.

• 5. The 95% back-transformed (from logit-scale) Wald confidence intervals generally have a non-coverage rate close to the nominal 5%. However, for small values of p _gs they are highly asymmetrically distributed (with respect to p _gs). Intervals with lower bounds exceeding p _gs dominate in these cases. If p _gs = 0, estimates of p _gs on the logit scale tend to −∞, and the approximate standard errors are badly determined, resulting in useless confidence intervals. For high values of p _gs, intervals with upper bounds lower than p _gs get the upper hand. The back-transformed Wald confidence intervals are usable for p _gs ≥ 0.5, and tend to be conservative then.

• 6. The standard error of $D_{2}^{\rm mle}$ decreases with larger expected fragment counts, as expected. For all three types of confidence intervals larger numbers of fragments result in narrower confidence intervals.

• 7. None of the three types of confidence intervals are usable for all values of p _gs. The profile likelihood intervals have the broadest range of application of p _gs:p _gs < 0.7 irrespective of m, and p _gs ≥ 0.7 for larger values of m. The back-transformed Wald intervals perform best for large values of p _gs. The Wald confidence intervals are widest (at p _gs = 0.5 and 0.7), making them the least attractive in this range.

• 8. For all cases with p _gs ≥ 0.3, $D_{2}^{\rm mle}$ has smaller standard errors than $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$. Furthermore, in all cases the profile likelihood confidence intervals based on $D_{2}^{\rm mle}$ are narrower than the bootstrap confidence intervals based on $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$. These results suggest that $D_{2}^{\rm mle}$ is to be preferred over the modified coefficients $D_{{\bar{L}}}^{\rm mod}$ and $D_{L}^{\rm mod}$.

Comparing standard errors

The simulation study has shown that the proposed estimators are approximately unbiased. Although attractive in itself, unbiasedness does not guarantee a higher precision since ${\text{SE}} = \sqrt {{\text{bias}}^{2} + \text{var} }$. Using the data from the simulation study, we estimated ${\text{bias}}\left( D \right)$, and ${\text{var}}\left( D \right)$ by bootstrapping, and compared ${\text{SE}}\left( D \right)$ with ${\text{SE}}\left( {D_{L}^{\rm mod} } \right)$.

For most cases we find ${\text{SE}}\left( D \right)$ > $SE\left( {D_{L}^{\rm mod} } \right)$, with the most extreme outcome for p _gs = 0.0 and m = 120, where ${\text{SE}}\left( D \right)$ is $4. 5\times {\text{SE}}\left( {D_{L}^{\rm mod} } \right)$. For large values of p _gs (p _gs = 0.95, all m; p _gs = 0.9, m = 40,70; p _gs = 0.7, m = 40), we find that ${\text{SE}}\left( D \right)$ < ${\text{SE}}\left( {D_{L}^{\rm mod} } \right)$, but ${\text{SE}}\left( D \right)$ is never smaller than $0. 9 5\times {\text{SE}}\left( {D_{L}^{\rm mod} } \right)$. Hence, depending on the combination of p _gs and m, very large gains in standard error can be obtained, or, for large p _gs (in combination with small fragment counts) minor losses. In the last cases, the gain in bias is outweighed by the loss in variance, and the new estimator $D_{L}^{\rm mod}$ is marginally less precise compared to D.

Results for the effect of expected number of fragments on precision

Figure 2 shows the results of the simulation study on the relationship between the expected number of fragments m and precision of $D_{2}^{\rm mle}$. In the left-hand side figure the expected number of fragments is plotted against the average standard error of $D_{2}^{\rm mle}$. At the top axis the average band count is shown. We observe the following:

• 1. Starting at small numbers of fragments, the standard error of $D_{2}^{\rm mle}$ decreases as the number of fragments increases. The rate of change of the standard error is high at low fragment counts, but decreases. As the number of fragments increases, the standard error reaches a minimum, and afterwards increases again.

• 2. The optimal number of fragments depends on p _gs. Smaller values of p _gs allow smaller numbers of fragments. For p _gs = 0 or 0.1 the optimal number of fragments is close to m = 140 (or n = 110 bands). For p _gs = 0.3 this count is approximately m = 250 (n = 165), for p _gs = 0.5 m = 350 (n = 205), and for p _gs = 0.7 m = 500 (n = 245). For p _gs = 0.9 or 0.95 the optimal fragment count is larger than 500 fragments.

• 3. In general a large range of near-optimal fragment counts exists.

• 4. The usual range of band counts (between 50 and 100) is not optimal, especially if the focus is on highly related species with high p _gs. However, the gain in accuracy will generally be small if larger band counts are used. The small gain in accuracy must be balanced against the possible scoring problems that may occur with large band counts.

In the right-hand side figure the expected number of fragments is plotted against the average $D_{2}^{\rm mle}$, and average Dice similarity. Furthermore, the average lower and upper bounds of the 95% profile likelihood confidence intervals are shown. For clarity, only results for p _gs = 0.1, 0.5, and 0.9 are given. We observe the following:

• 5. $D_{2}^{\rm mle}$ is an (almost) unbiased estimator of p_gs, even for extremely large fragment counts. For very small fragment counts (m ≤ 25) there appears to be small negative bias.

• 6. Starting at small m, the width of the confidence interval quickly decreases. For large enough m (depending on p _gs) the width remains approximately constant.

• 7. The usual range of band counts, although not optimal, seems reasonable. Only little gain in the width of the confidence intervals can be expected from higher fragment counts, as in 4).

• 8. The confidence intervals are rather wide. The only way to reach narrower intervals is to use multiple gels with different primer combinations, and combine the information from the different profiles.

Fig. 2

a Average SE of $D_{2}^{\rm mle}$, and b average $D_{2}^{\rm mle}$ and D, as functions of numbers of fragments for different values of p_gs. In plot a interpolated lines are drawn for fragment counts ranging from 15 to 500 in steps of 5 for p_gs = 0, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95, and in plot b for p_gs = 0.1, 0.5, and 0.9. The shaded areas in b indicate average 95% profile likelihood confidence intervals of p_gs. For each value of m and p_gs, 10,000 pairs of profiles were sampled from fldF_S with scoring range 51–500. The top axes show the average number of bands on a non-linear scale

Results for case study on lettuce and related genera

Figure 3 shows the UPGMA dendrograms for the five species, split out for the three dissimilarity measures. The dendrograms for 1 − D and 1 − J are largely the same. With all three dissimilarities the species are separated well. Notice that the 1 − D ^mle dissimilarities are closer to 0, as expected. Notice further that the 1 − D ^mle dissimilarities are not a simple shift towards 1. In the hierarchical clustering scheme for D and J, L. tenerrima joins after clustering of L. serriola, L. sativa, and L. tatarica, but for D ^mle L. tenerrima joins after clustering of L. serriola and L. sativa only. Apparently, L. tenerrima and L. tatarica have switched places. This behavior can be understood from the band count. The AFLP profiles for L. tenerrima contain a small number of bands, whereas L. tatarica profiles have large counts. Hence, bias corrections for comparisons with L. tenerrima are smaller than those with L. tatarica.

Fig. 3

UPGMA dendrograms for three dissimilarities: a 1−Dice D, b 1−Jaccard J, and c 1−D ^mle for five species of Lactuca and related genera, with 6–9 accessions per species. Labels are: ten = L. tenerrima, mur = M. muralis, ser = L. serriola, sat = L. sativa, and tat = L. serriola. For D ^mle we used fld F _S with scoring range 110–501

Conclusions and discussion

In this study, we propose new estimators of pairwise genetic similarity p _gs from binary AFLP data, correcting for homoplasy. We define pairwise genetic similarity for AFLP data as the weighted average of fractions of common fragments. Using this definition, the Dice coefficient is a natural candidate for replacement, but a homoplasy corrected version of the Jaccard coefficient is suggested as well. For most practical cases the new estimators are better than the ordinary Dice coefficient, because the bias is removed, at the cost of a small increase in variance. Only for large genetic similarities in combination with low band counts (roughly: p _gs = 0.95 and n < 100, p _gs = 0.90 and n < 65, p _gs = 0.70 and n < 38), Dice performs better.

For profiles without band length information, we propose the modified Dice coefficient $D_{{\bar{L}}}^{\rm mod}$. Using the bootstrap, standard errors and confidence intervals are obtained. The bootstrap allows a further reduction of the already small negative bias of $D_{{\bar{L}}}^{\rm mod}$.

For AFLP profiles with band length information, we have three candidate estimators: $D^{\rm mle}$, $D_{L}^{\rm mod}$, and $D_{{\bar{L}}}^{\rm mod}$. Best results are obtained using the maximum likelihood estimator $D^{\rm mle}$, although differences are small. Second best is, surprisingly, $D_{{\bar{L}}}^{\rm mod}$, ignoring the band length information. The standard error of $D^{\rm mle}$ follows from likelihood theory, hence no bootstrapping is needed. Profile likelihood confidence intervals for p _gs are narrowest. However, care has to be taken in the choice of type of confidence interval. Profile likelihood intervals are only acceptable, if p _gs < 0.7 irrespective of the number of fragments, and for p _gs ≥ 0.7 if the fragment counts are large enough. For small fragment counts and large p _gs, more acceptable results are obtained for the back transformed Wald intervals, using an estimator on the logit-scale.

The modified Dice coefficients $D_{{\bar{L}}}^{\rm mod}$ or $D_{L}^{\rm mod}$ are good alternatives as well. Over the whole range of p _gs the confidence intervals based on $D_{L}^{\rm mod}$ and $D_{{\bar{L}}}^{\rm mod}$ showed more stable coverage properties than those for $D^{\rm mle}$.

The homoplasy corrected estimate of genetic similarity is always smaller than the ordinary Dice coefficient, because part of the observed band similarity is attributed to chance. The magnitude of this correction depends on the true genetic similarity, but also on the fragment counts. Both smaller similarities and larger numbers of fragments lead to larger corrections.

The standard error of the similarity estimator $D^{\rm mle}$ and the width of the confidence interval cannot be made arbitrarily small by increasing the number of fragments in the profiles. The optimal number of fragments exists, but its value depends on the true genetic similarity, and there is a large range of near-optimal fragment counts. The usual range of band counts (between 50 and 100) is suboptimal, but in general the gain in precision is small if higher numbers of fragments are used, and should be balanced against increasing scoring problems.

To get more precise estimates of genetic similarity, multiple gels with different primer combinations or restriction enzymes should be used, and the information from the different profiles should be combined. $D^{\rm mle}$ can easily be modified to estimate a single genetic similarity from multiple pairs of profiles, even allowing for possibly different fld’s for the different profiles. Modifications of this type (beyond ordinary averaging) are less straight forward for the modified coefficients $D_{L}^{\rm mod}$ and $D_{{\bar{L}}}^{\rm mod}$. This flexibility is a further argument in favor of $D^{\rm mle}$.

To account for homoplasy and collisions properly, all bands in the profiles must be scored, not just the non-monomorphic bands. The effect of scoring non-monomorphic bands only is that Dice and Jaccard coefficients are lowered in a way that depends on the set of individuals under study. Inclusion or exclusion of a less related individual in the study, could result in exclusion or inclusion of bands, which are polymorphic with the individual, but monomorphic without. Hence, the similarity coefficient would be different with or without this individual.

Conclusions drawn here are mainly based on a single simulation study. Furthermore, we have to rely on a number of assumptions. For instance, we assume to know the fld, which in reality hardly ever is the case. Only if full DNA sequence information is available and by using in-silico AFLP procedures, do we have an estimate of the fld very close to the true fld. In other cases, a less reliable estimate of the fld may come from the GC content or directly from the binary AFLP data, as described in Gort et al. (2006).

Another topic related to the fld, is the fact that two distantly related individuals, e.g. with highly different GC contents, may have different flds. In this paper we have assumed that there is a common fld. Further study on the effect of misspecification of the flds on the statistical properties of the proposed estimators is needed.

In the present paper, we studied the effect of homoplasy and collision on the estimation of genetic similarity from binary AFLP data. Examples of studies that may directly benefit from the proposed homoplasy corrected estimates of genetic similarity are studies on genetic diversity, e.g. in plant genetic resources or breeding programs, but also phylogenetic and taxonomic studies, and studies of essential derivation, in which plant breeders try to establish thresholds for genetic similarity between initial and new, allegedly derived varieties (Van Eeuwijk and Law 2004).

In other studies where AFLP profiles are analyzed, the problem of homoplasy may have an impact as well. For example, in linkage studies for tracing quantitative trait loci (QTLs) or for mapping purposes, a band is interpreted as a single DNA fragment, residing at one unique locus of the genome. Here the best strategy may be to avoid homoplasy as much as possible, by limiting the number of fragments per lane, or avoiding bands corresponding to short fragments.

In population genetic applications of AFLP, homoplasy and collision may also affect estimation of parameters. For example, if the allele frequency of the DNA fragment corresponding to a band is the parameter of interest, like in Krauss (2000), who tested three procedures for estimation of null allele frequencies, homoplasy may cause some bands to be non-homologous, thereby changing the relative frequency of absent bands. Derived quantities like heterozygosity, coefficient of co-ancestry, or genetic distances, may need corrections for homoplasy and/or collision as well. These corrections require careful consideration, and are beyond the scope of the present paper. An example of a recent study of homoplasy in population genetics is Caballero et al. (2008), who focus on population genetic diversity and detection of selective loci.

In a study by Holland et al. (2008) about automated scoring of AFLPs, the suggestion is made to decrease the bin width for scoring fragments on a capillary system. This is another route towards a solution of the homoplasy problem, because the resulting profiles will likely have less homoplasy, albeit at the cost of an increased error rate for homologous fragments. In future work this approach may be joined with ours to arrive at improved evaluation of homoplasy.

The problem of homoplasy described here is not limited to the AFLP marker system. In a study on homology among RAPD fragments for three very closely related species of sunflowers, Rieseberg (1996) reports that of 220 pairwise comparisons of comigrating fragments only 79% identified loci useful for comparative genetic studies. For RAPD comparable corrections for homoplasy can be envisioned, as we propose here for AFLP.

Software in R (R Development Core Team 2005) for calculation of the proposed estimators is available from the authors.

Appendices

Appendix 1: Comparison of bootstrap confidence intervals

We compare three types of bootstrap confidence intervals (c.i.):

• simple percentile c.i.

• bias-corrected percentile c.i.

• accelerated bias-corrected percentile (BC _a ) c.i.

These c.i.’s are calculated as described in (Manly 1997), pp. 39–56. For the accelerated bias-corrected percentile c.i.’s calculation of the constant a _acc is required. Manly (1997) suggests to approximate a _acc by $\sum\nolimits_{j = 1}^{N} {(\hat{\Uptheta }_{.} - \hat{\Uptheta }_{ - j} )^{3} } /[6\{ \sum\nolimits_{j = 1}^{N} {(\hat{\Uptheta }_{.} - \hat{\Uptheta }_{ - j} )^{2} } \}^{1.5} ]$ with $\hat{\Uptheta }_{ - j}$ the partial estimate of the parameter $\Uptheta$ based on all but the jth observation, and $\hat{\Uptheta }_{.}$ the average of $\hat{\Uptheta }_{ - j}$ (j = 1,…, N). In our case the parameter $\Uptheta$ is the fraction of common fragments p _gs, estimated by either $D_{{\bar{L}}}^{\rm mod}$ or $D_{L}^{\rm mod}$.

For $D_{L}^{\rm mod}$ we take a pair of binary scores (y _1j , y _2j ) (j = 1,…, N) to be an observation. The constant a _acc is calculated by removing observation j from the pair of profiles, rescaling the fragment length distribution, calculating $D_{L}^{\rm mod}$ from the reduced dataset, and repeating over all band positions (j = 1,…, N), resulting in partial estimates $\hat{\Uptheta }_{ - j}$.

For $D_{{\bar{L}}}^{\rm mod}$ the information on band lengths is missing, and a pair of profiles can be summarized as a vector of counts (a, b, c, d). The observations are the pairs of binary scores 1–1 (occurring a times), 1–0 (b times), 0–1 (c times), and 0–0 (d times). The partial estimates $\hat{\Uptheta }_{ - j}$ consist of weighted averages [with weights (a, b, c, d)] of $D_{{\bar{L}}}^{\rm mod}$ values. We label the weighted averages $\hat{\Uptheta }_{ - j}^{a}$ (occurring a times), $\hat{\Uptheta }_{ - j}^{b}$ (b times), $\hat{\Uptheta }_{ - j}^{c}$ (c times), and $\hat{\Uptheta }_{ - j}^{d}$ (d times). $\hat{\Uptheta }_{ - j}^{a}$ is the weighted average of the 4 $D_{{\bar{L}}}^{\rm mod}$ values calculated for the profile pairs (a, b, c, d), (a − 1, b + 1, c, d), (a − 1, b, c + 1, d), (a − 1, b, c, d + 1), $\hat{\Uptheta }_{ - j}^{b}$ is calculated from profile pairs (a + 1, b − 1, c, d), (a, b, c, d), (a, b − 1, c + 1, d), (a, b − 1, c, d + 1), $\hat{\Uptheta }_{ - j}^{c}$ from profile pairs (a + 1, b, c − 1, d), (a, b + 1, c − 1, d), (a, b, c, d), (a, b, c − 1, d + 1), and $\hat{\Uptheta }_{ - j}^{d}$ from profile pairs (a + 1, b, c, d − 1), (a, b + 1, c, d − 1), (a, b, c + 1, d − 1), (a, b, c, d).

For the simulation dataset with 10,000 replicates, we calculated 95% bootstrap c.i.’s for $D_{{\bar{L}}}^{\rm mod}$, based on a bootstrap resample size of 1000. The results are shown in Table 5. The non-coverage rates for the 95% simple percentile c.i. range from 0.0497 to 0.0915 (average 0.0581), a bit larger than the nominal 0.05. The larger error rates occur for the profiles with smallest expected fragment counts (m = 40), and extreme values of p _gs (p _gs = 0.0, 0.9, 0.95). In general the c.i.’s are slightly too narrow. The 95% bias-corrected percentile c.i.’s have better non-coverage rates, ranging from 0.0475 to 0.0707 (average 0.0550). The non-coverage rates of the 95% BC _a c.i.’s range from 0.0383 to 0.0545 (average 0.0486). This last method seems to be a bit too conservative, delivering intervals which are slightly too wide. Over the whole range of p _gs values this last method performed best.

For the same simulation data we calculated 95% bootstrap c.i.’s for $D_{L}^{\rm mod}$ (see Table 6). The non-coverage rates for the simple percentile method range from 0.0514 to 0.0878 (average 0.0584), for the bias-corrected method from 0.0499 to 0.065 (average 0.0548), and for the accelerated bias-corrected method from 0.0378 to 00555 (average 0.0487). Again, the accelerated bias-corrected method performs best with slightly conservative c.i.’s.

Appendix 2

See Table 7 for a list of used symbols.

Table 7 Overview on symbols